The Bizarreness of Optimization

Background: consider the hashtable with closed addressing/separate chaining:

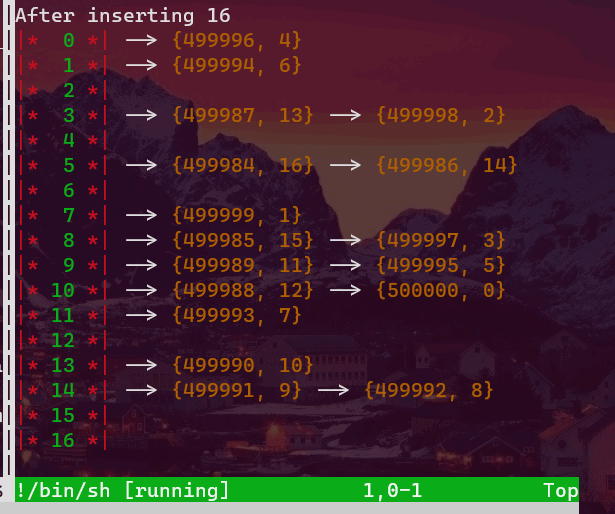
Typically, we can have two different schemes to link through all the nodes. One is to link the last node of the current bucket to the first node of the next non-empty bucket. See the above picture and imagine taht there are links among these buckets. Another is to make all the nodes look exactly the same as the above picture (by which I mean to link the tail nodes with null pointers).

The second approach will have some more work to obtain the successor of the current node. It may need to scan a lot of (empty) buckets to get its successor. Sounds awful, huh? Actually not. By amortized analysis (assume the max_load_factor==1 ), ideally, we will have each node in a (different) bucket exactly. So it can be efficient.

How about the first one? The bad news is that it can suffer from very terrible insertion overhead. Now imagine you have a very big hashtable, tab[i] and tab[j] are two adjacent (non-empty) buckets. The horrible thing is that you have a very big difference |i-j|, and then an item whose hash code k is between i and j is needed to be inserted there. We will need to scan all the way down from k to j in order to update the links of the three nodes: the last node of bucket i, the newly inserted node, the first node of bucket j (you can think of this process as the insertion of a doubly-linked list). And if we constantly perform this pathological operation, j-1, i+1, j-2, i+2,..., things can get really bad, bad, bad, bad.

The Problem: Now if I ask you a simple question, after building a hashtable, we iterate through all the elements, which do you think is faster, the all-linked-up one (1st case) or the only-in-bucket-linked one (2nd case)?

Here is a piece of test code and the whole code can be found here.

int main()
{
#if   defined(USE_HASHMAP)
    mySymbolTable::HashMap<int, int> mp{};
#elif defined(USE_HASHMAP2)
    mySymbolTable::alternative::HashMap<int, int> mp{};
#else
    std::unordered_map<int, int> mp{};
#endif

    constexpr int N = 1'000'000;
    int k = 0;

    for(int i=0; i < N; ++i)
        mp[N-i] = i;

    auto t1 = std::clock();
    for(auto it=mp.begin(); it!=mp.end(); ++it)
        ++k;
    auto t2= std::clock();

    auto iteration_time_elapsed = (t2 - t1) / (double)1'000;
    std::cout << "Iterating through " << k << " items used "
              << iteration_time_elapsed << "ms\n";
    return 0;
}

Essentially, they run the following code respectively

_self& operator++() {
    _ptr = _ptr->_next;
    return *this;
}

vs

_self& operator++() {
    auto next = _table->next_entry(_ptr, _bucket_index);
    _ptr = next.first;
    _bucket_index = next.second;
    return *this;
}

std::pair<node_ptr, size_t> next_entry(node_ptr x, size_t bucket_index) const {
    assert(x != nullptr && "cannot increment end() iterator");
    if (x->_next) return { x->_next, bucket_index };
    size_t i = bucket_index + 1;
    for (; i < _hashtable.size(); ++i) {
        if (_hashtable[i]) return { _hashtable[i], i };
    }
    return { nullptr, i };
}

So, which one? (I think it should the first one, any rational human beings would make this choice, I suppose. Don’t believe it??)

Now have a look at their assembly code

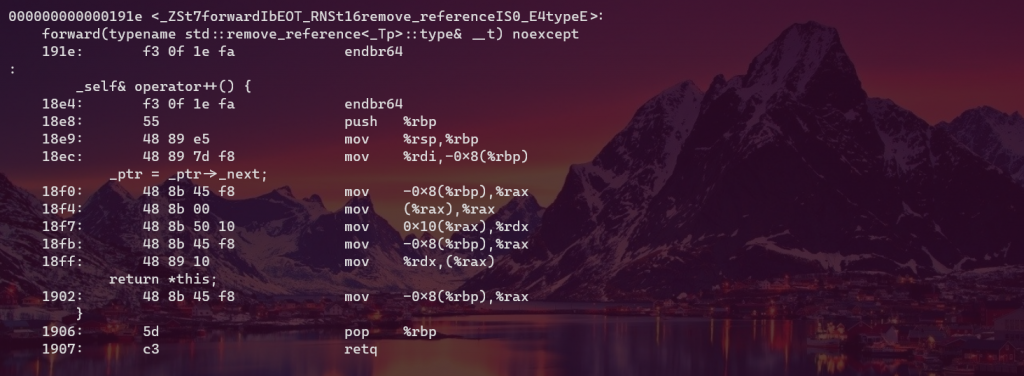
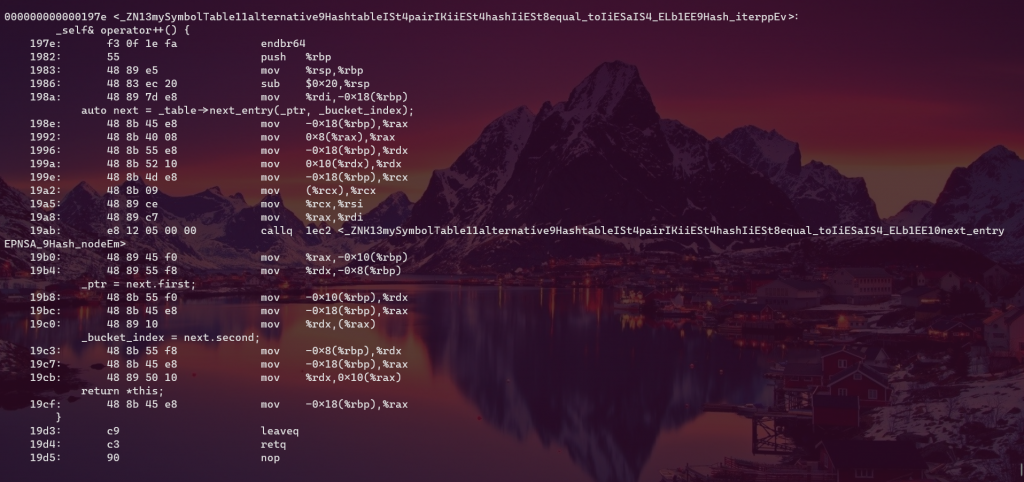
The bizarre thing is that in debug mode (-g flag), the 1st case beats the 2nd by about one fifth (t1 = 82% * t2 ). While if optimization is enabled (-O3 flag), it’s a whole different story. The summary table is given below.

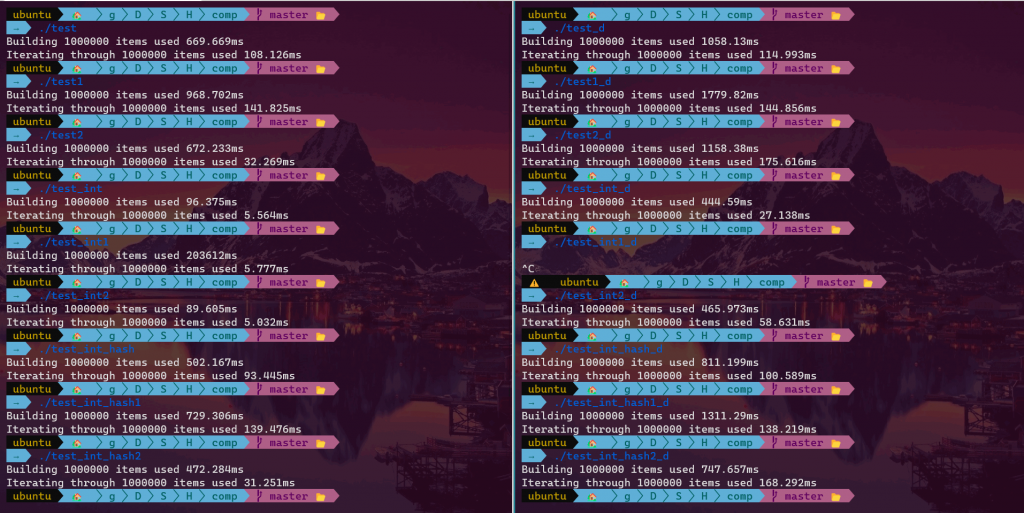
Here, _d suffix means debug version, *1 suffix means myst::HashMap (1st case), *2 suffix means myst::alternative::HashMap (2nd case), and no suffix suggests we are using std::unordered_map.

We can see from the results that optimization -O3 barely boosts the performance of the 1st case (std::unordered_map and myst::HashMap) except the test_int cases, but rather make a significant boost in the 2nd case (myst::alternative::HashMap). Given the 2nd is a little bit more complicated, it is therefore expected there will be more space for the 2nd case to optimize, for example, inlining. Still, I don’t think it can beat the 1st small code. How do we explain this weird phenomenon?

(In my understanding, small code means fast, think about cache, and technically speaking, 2nd case should never be faster than the 1st one.)